最后一遍-L42-Trapping Rain Water
描述:
Given n non-negative integers representing an elevation map where the width of each bar is 1,
compute how much water it can trap after raining.
Example 1:
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1].
In this case, 6 units of rain water (blue section) are being trapped.
Example 2:
Input: height = [4,2,0,3,2,5]
Output: 9
Constraints:
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105
传说中的“接雨水”这道题目,思考的过程,查看了discuss
Here’s how we can arrive at this solution: //具体思路
Let’s think about the absolute simplest case: we’ve got a [2,1,3] array, telling us that we can trap 1 block of rainwater.
【2,1,3】 是一个简单的场景,就是一个凹型的数组结构
How we arrive to this, is pretty simple, we know that because we’ve got a two at the beginning,
但是我们为什么一眼就能看出这个【2,1,3】可以盛水,在于我们知道了两边
we can only fill up to two blocks of water per point, and we know that we can only do that at a point after two, and we know that we can do it at all because 3, at the end of the array, would be able to contain the water, so we can add water until we get to 3, and can only add 2 - the height of the point.
因为只有3个元素,第三个元素明显比第二个高,而且第一个也比第二个高,这个第二个形成的凹性,就能够存储水。
So, if we had something a little more complex, like [2, 1, 3, 1, 4], we could fill up to the 3 optimally, and then repear the same algorithm from the 3 onward.
如果是这种情况下,就能够继续按照上述的思路,继续的计算盛装的水
However, if we had, instead, [2, 1, 3, 1, 2] we would fill up to the 3, and then see that we cannot fill over to the 2 because we would overflow, so we instead mirror the algorithm and bring from the 2 backward.
class Solution {
public int trap(int[] height) {
if (height == null || height.length == 0) {
return 0;
}
int left = 0; int right = height.length - 1; // Pointers to both ends of the array.
int maxLeft = 0; int maxRight = 0;
int totalWater = 0;
/**
* 首先是 h[left] < h[right] ==> maxLeft 赋值(初始化的非常的优雅),然后和h[left]比较:
* 如果比maxLeft大,说明不能存储水
* 如果比maxLeft小,加上一开始的判断: h[left] < h[right],说明可以存储水,并且只计算:maxLeft到left之间的存储量
* */
while (left < right) {
// Water could, potentially, fill everything from left to right, if there is nothing in between.
if (height[left] < height[right]) {
// If the current elevation is greater than the previous maximum, water cannot occupy that point at all.
// However, we do know that everything from maxLeft to the current index, has been optimally filled, as we've
// been adding water to the brim of the last maxLeft.
if (height[left] >= maxLeft) {
// So, we say we've found a new maximum, and look to see how much water we can fill from this point on.
maxLeft = height[left];
// If we've yet to find a maximum, we know that we can fill the current point with water up to the previous
// maximum, as any more will overflow it. We also subtract the current height, as that is the elevation the
// ground will be at.
} else {
totalWater += maxLeft - height[left];
}
// Increment left, we'll now look at the next point.
left++;
// If the height at the left is NOT greater than height at the right, we cannot fill from left to right without over-
// flowing; however, we do know that we could potentially fill from right to left, if there is nothing in between.
} else {
// Similarly to above, we see that we've found a height greater than the max, and cannot fill it whatsoever, but
// everything before is optimally filled
if (height[right] >= maxRight) {
// We can say we've found a new maximum and move on.
maxRight = height[right];
// If we haven't found a greater elevation, we can fill the current elevation with maxRight - height[right]
// water.
} else {
totalWater += maxRight - height[right];
}
// Decrement left, we'll look at the next point.
right--;
}
}
// Return the sum we've been adding to.
return totalWater;
}
}
第二种更加好理解的思路:
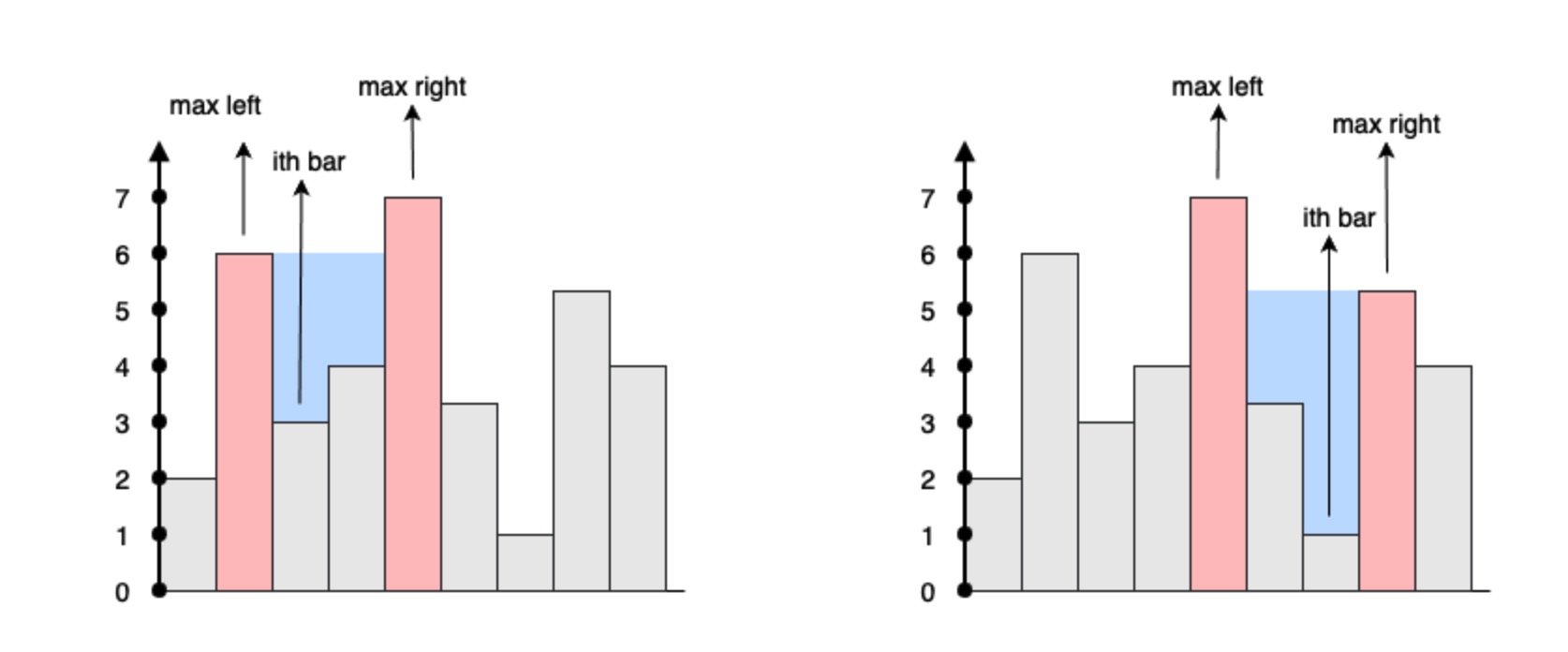
A ith bar can trap the water if and only if there exists:
a higher bar to the left
a higher bar to the right of ith bar
To calculate how much amount of water the ith bar can trap,
we need to look at:
the maximum height of the left bar
the maximum height of the right bar
then The water level can be formed at ith bar is:
waterLevel = min(maxLeft[i], maxRight[i])
If waterLevel >= height[i] then ith bar can trap waterLevel - height[i] amount of water.
To achieve in O(1) when looking at the maximum height of the bar on the left side and on the right side of ith bar, we pre-compute it:
Let maxLeft[i] is the maximum height of the bar on the left side of ith bar.
Let maxRight[i] is the maximum height of the bar on the right side of ith bar.
示例图如下:
class Solution {
public int trap(int[] height) {
int n = height.length;
int[] leftMax = new int[n], rightMax = new int[n];
// 比较的逻辑中,leftMax是一个数组,Math.max(height[i-1], leftMax[i-1]) 非常好的一个表述
for (int i = 1; i < n; ++i)
leftMax[i] = Math.max(height[i-1], leftMax[i-1]);
for (int i = n-2; i >= 0; --i)
rightMax[i] = Math.max(height[i+1], rightMax[i+1]);
int ans = 0;
for (int i = 0; i < n; ++i) {
int waterLevel = Math.min(leftMax[i], rightMax[i]);
if (waterLevel >= height[i]) ans += waterLevel - height[i];
}
return ans;
}
}